Linear classifier using least square approach in Pyhton

Sample Data:-  Use following data set 1 and data set-2 for classifier using least square approach

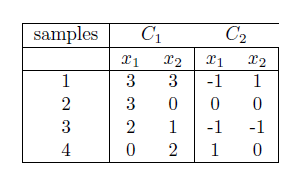Data Set -1

Data Set -2

Problem statement :- Sample program to find the linear classifier using least square approach.

import sys
import matplotlib.pyplot as plt
import pylab as pl
import numpy as np

def getMultiplePoints(x,y,weight,boundX1,boundX2):
 x1 =[x,0]
 x2 =[0,y]
 pointsX = []
 pointsY = []
 pointsX.insert(1,y)
 pointsX.insert(2,0)
 pointsY.insert(1,0)
 pointsY.insert(2,x)
 #for boundX1
 pointsX.insert(0,boundX1)
 temp = -(weight[0]*boundX1 + weight[2])/weight[1]
 pointsY.insert(0,temp)
 #for boundX2
 pointsX.insert(3,boundX2)
 temp = -((weight[0]*boundX2) + weight[2])/weight[1]
 pointsY.insert(3,temp) 
 return (pointsX,pointsY)

#plot points 
def getCoordinatesList(dataset,weightPlot):
 XList1 =[]
 YList1 =[]
 XList2 =[]
 YList2 =[] 
 count = 0
 boundX = -4
 boundY =  4
 #compute classifier co-ordinates
 x1 = - (weightPlot[2]/weightPlot[1])
 y1 = 0
 x2 = 0
 y2 = - (weightPlot[2]/weightPlot[0])
 itr = len(dataset)/2
 # compute some random point with slope as W and bias b 
 plotTup = getMultiplePoints(x1,y2,weightPlot,boundX,boundY)
 for row in dataset:
  if(count< itr):
   XList1.append(row[0])
   YList1.append(row[1])
  else:
   XList2.append(row[0])
   YList2.append(row[1])
  count = count+1
 return (XList1, YList1,XList2, YList2,plotTup)

def plotDataPointsAndClassifier(plotData,weightPlotLS):
 boundX = -4
 boundY =  4
 colorLS = 'black'
 (XList1, YList1,XList2, YList2,plotTupLS) =
  getCoordinatesList(plotData,weightPlotLS)
 #Draw points with red and Blue color 
 plt.plot(XList1, YList1, 'ro',XList2, YList2, 'bo')
 plt.axis([boundX, boundY, boundX, boundY])
 plt.plot(plotTupLS[0],plotTupLS[1],color = colorLS,label='Least Square')
 plt.legend(loc='best') 
 plt.show()
 
def compute(row, weights):
 bias = weights[2]
 output = bias
 for i in range(len(row)-1):
  output += weights[i] * row[i]
 if row[2] == 1 and output > 0:
  return True
 elif row[2] == -1 and output <= 0: 
  return True
 else:
  return False 

#compute b to such data data point are segrated 
def getB(dataset,weights):
 flag = True
 epoch = 1
 while(True):
  flag = False ; epoch = epoch + 1
  for row in dataset:
   prediction = compute(row, weights)
   if not prediction:
    weights[2] = row[2] -(weights[0]*row[0]+weights[1]*row[1])
    flag = True
  if epoch == 10 or flag == False : 
   break
 return weights
 
# To find classifier Minimum Squared Error Procedures - using Pseudoinverse
def LeastSquareClassifier(inputData):
 #Compute b based on input size. B is 1x<size> matrix with 1
 size = len(inputData)
 b = [1 for x in range(size)]
 #find b's transpose - > 8x1 matrix 
 bt = np.matrix(b).getT()
 #Prepare input matrix from dataset 
 m = np.matrix(inputData)
 #find tranpose of input matrix
 t = m.getT()
 #Multiply transpose of input matrix and matrix -  (Y^tY)
 mul = t*m
 #find inverse of outcome of above operation - (Y^tY)^-1 
 inv = mul.getI()
 # Find pseudo inverse- Multiply inversed matrix with 
 #transpose of input matrix - (Y^tY)^-1Y^t
 secondMul = inv * t
 #find solution matrix - Multiply pseudo matrix with b
 f = secondMul * bt
 #compute weight for ploting classifier 
 weightPlot = []
 weightPlot.insert(0,f.item(1))
 weightPlot.insert(1,f.item(2))
 weightPlot.insert(2,f.item(0))
 return weightPlot

def ClassifierOnTable1():
 #Find least square classifier weight 
 inputData = [[1,3,3], [1,3,0],[1,2,1] ,[1,0,2] ,
   [-1,1 ,-1],[-1,0, 0],[-1,1,1],[-1,-1 ,0]]
 plotData =  [[3,3,1], [3,0,1],[2,1,1] ,[0,2,1] ,[-1 ,1,-1],
   [0, 0,-1],[-1,-1,-1],[1,0,-1]]
 # find classifier for given dataset and Plot it. 
 weightPlotLS = LeastSquareClassifier(inputData)
 #plot data points and classifier 
 plotDataPointsAndClassifier(plotData,weightPlotLS)
 
def ClassifierOnTable2():
 inputData = [[1,3,3], [1,3,0],[1,2,1] ,[1,0,1.5] ,
   [-1,1 ,-1],[-1,0, 0],[-1,1,1],[-1,-1 ,0]]
 plotData  = [[3,3,1], [3,0,1],[2,1,1] ,[0,1.5,1] ,[-1 ,1,-1],
   [0, 0,-1],[-1,-1,-1],[1,0,-1]]
 # find classifier for given dataset and Plot it. 
 weightPlotLS = LeastSquareClassifier(inputData)
 #plot data points and classifier 
 plotDataPointsAndClassifier(plotData,weightPlotLS)

# map the inputs to the function blocks
options = {
  1 : ClassifierOnTable1,
  2 : ClassifierOnTable2,
 }
#start
if __name__ == '__main__':
 Dataset1C1 = [ [3,3], [3,0],[2,1] ,[0,1.5]]
 Dataset1C2 = [[-1 ,1],[0, 0],[-1,-1],[1 ,0]]
 print "1. LeastSquareClassifier on Data points in Table 1 \n \
  2. LeastSquareClassifier) on Data points in Table 2 \n"
 print "Enter your choice:\t"
 num = int(raw_input())
 options[num]()

Sample Output :-
[zytham@s158519-vm perceptron]$ python LSP.py
1. LeastSquareClassifier on Data points in Table 1
2. LeastSquareClassifier) on Data points in Table 2

Enter your choice:
1

[zytham@s158519-vm perceptron]$ python LSP.py 

1. LeastSquareClassifier on Data points in Table 1 

 2. LeastSquareClassifier) on Data points in Table 2 

Enter your choice: 

2